This article is a continuation of the Series on FreeRTOS and carries the discussion on FreeRTOS and its usage. The aim of this series is to provide easy and practical examples that anyone can understand. In our previous tutorial, we have seen How to use the Binary semaphore with ISR and without ISR. Today we will see the FreeRTOS Counting Semaphore Tutorial in LPC2148. Let’s start.
Table of Contents
Suggestion to read
- RTOS Basics – Part 1
- RTOS Basics – PART 2
- FreeRTOS Porting for LPC2148
- LPC2148 UART Tutorial
- LPC2148 Binary Semaphore
FreeRTOS Counting Semaphore Tutorial in LPC2148
Introduction
Before we starting this tutorial we should know about the semaphore. If you go through the RTOS Basics two parts you can go ahead. For others, I will give you a small introduction about semaphore.
Semaphore
A semaphore (sometimes called a semaphore token) is a kernel object that one or more threads of execution can acquire or release for the purposes of synchronization or mutual exclusion. This is useful when two or more tasks accessing the same resource. A binary semaphore used for synchronization does not need to be ‘given’ back after it has been successfully ‘taken’ (obtained).
A kernel can support many different types of semaphores, including
- binary,
- counting, and
- mutual‐exclusion (mutex) semaphores.
Binary Semaphore
- Similar to mutex
- Can have a value of 1 or 0
- Whenever a task asks for a semaphore, the OS checks if the semaphore’s value is 1
- If so, the call succeeds and the value is set to 0
- Else, the task is blocked
Binary semaphores are treated as global resources,
|
|
|
- They are shared among all tasks that need them.
- Making the semaphore a global resource allows any task to release it, even if the task did not initially acquire it?
Counting Semaphores
- Semaphores with an initial value greater than 1
- Can give multiple tasks simultaneous access to a shared resource, unlike a mutex
- Priority inheritance, therefore, cannot be implemented
Whenever we are giving semaphore from any task, then the semaphore count increases up to the maximum number that we have generated.
Applications of Counting Semaphore
Counting semaphores are typically used for two things:
- Counting events.
- Resource management.
Counting events
In this usage scenario, an event handler will ‘give’ the semaphore each time an event occurs, and a handler task will ‘take’ the semaphore each time it processes an event.
The semaphore’s count value will be incremented each time it is ‘given’ and decremented each time it is ‘taken’. The count value is therefore the difference between the number of events that have occurred and the number of events that have been processed. Semaphores created to count events should be created with an initial count value of zero, because no events will have been counted prior to the semaphore being created.
Resource management
In this usage scenario, the count value of the semaphore represents the number of resources that are available.
To obtain control of a resource, a task must first successfully ‘take’ the semaphore. The action of ‘taking’ the semaphore will decrement the semaphore’s count value. When the count value reaches zero, no more resources are available, and further attempts to ‘take’ the semaphore will fail.
When a task finishes with a resource, it must ‘give’ the semaphore. The action of ‘giving’ the semaphore will increment the semaphore’s count value, indicating that a resource is available, and allowing future attempts to ‘take’ the semaphore to be successful.
Semaphores created to manage resources should be created with an initial count value equal to the number of resource that are available.
APIs Used
xSemaphoreCreateCounting()uxSemaphoreGetCount()xSemaphoreGive ()xSemaphoreTake()
Here we have already know the last two APIs. Because we were already discussed in our previous tutorials.
|
|
|
xSemaphoreCreateCounting()
Creates a counting semaphore, and returns a handle by which the semaphore can be
referenced. Each counting semaphore requires a small amount of RAM that is used to hold the semaphore’s state. If a counting semaphore is created using xSemaphoreCreateCounting() then the required RAM is automatically allocated from the FreeRTOS heap. If a counting semaphore is created using xSemaphoreCreateCountingStatic() then the RAM is provided by the application writer, which requires an additional parameter, but allows the RAM to be statically allocated at compile time.
#include “FreeRTOS.h”
#include “semphr.h”
SemaphoreHandle_t xSemaphoreCreateCounting( UBaseType_t uxMaxCount,
UBaseType_t uxInitialCount );
To use Counting Semaphore you should add the below line in the FreeRTOSConfig.h
#define configUSE_COUNTING_SEMAPHORES 1
|
|
|
Parameters:
- uxMaxCount The maximum count value that can be reached. When the semaphore reaches this value it can no longer be ‘given’.
- uxInitialCount The count value assigned to the semaphore when it is created.
Return:
- NULL Returned if the semaphore cannot be created because there is insufficient
heap memory available for FreeRTOS to allocate the semaphore data structures. - Any other value The semaphore was created successfully. The returned value is a handle by which the created semaphore can be referenced.
uxSemaphoreGetCount()
This function returns the count of a semaphore.
Binary semaphores can only have a count of zero or one. Counting semaphores can have a count between zero and the maximum count specified when the counting semaphore was created.
#include “FreeRTOS.h”
#include “semphr.h”
|
|
|
UBaseType_t uxSemaphoreGetCount( SemaphoreHandle_t xSemaphore );
Parameters:
- xSemaphore : The handle of the semaphore being queried.
Return:
The count of the semaphore referenced by the handle passed in the xSemaphore parameter.
Code
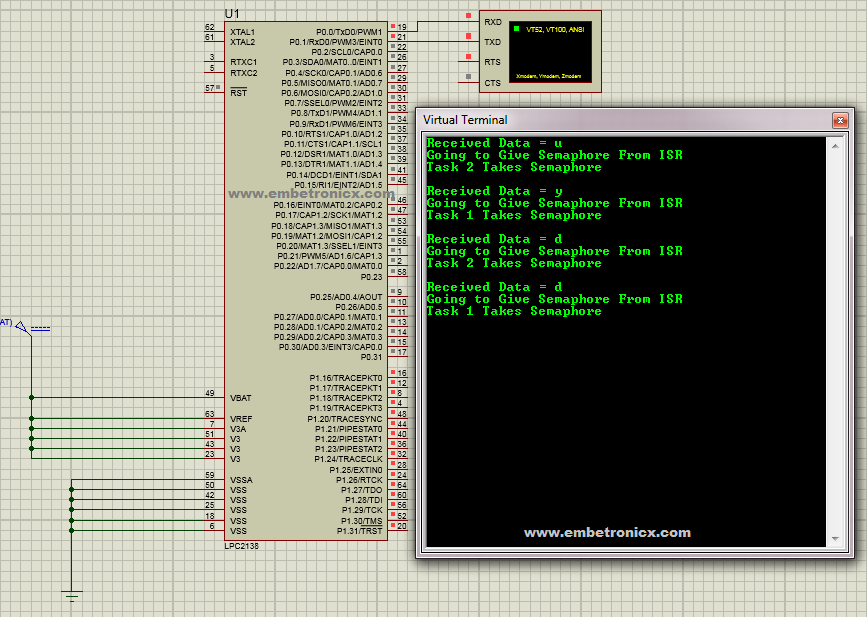
In this code, I’ve created two tasks and Counting Semaphore with the value of 3. So two tasks are waiting for the semaphore. Once an interrupt occurred, task 2 will take that semaphore and prints it. But task 1 is still waiting. So next occurrence of an interrupt, task 1 takes the semaphore and prints. Here I’m adding only the main file. If you want to download the full project, please visit here (GitHub).
|
|
|
#include <stdlib.h>
#include "FreeRTOS.h"
#include "task.h"
#include "serial.h"
#include "semphr.h"
void initpll(void);
void task1(void *p);
void task2(void *p);
xSemaphoreHandle countingsemaphore;
int main()
{
initserial();
countingsemaphore=xSemaphoreCreateCounting(3,0);
xTaskCreate(task1,"task1",128,NULL,1,NULL);
xTaskCreate(task2,"task2",128,NULL,1,NULL);
vTaskStartScheduler();
while(1);
}
void initpll(void)
{
PLL0CON=0x01;
PLL0CFG=0x24;
PLL0FEED=0xAA;
PLL0FEED=0x55;
while(!(PLL0STAT&1<<10));
PLL0CON=0x03;
PLL0FEED=0xAA;
PLL0FEED=0x55;
VPBDIV=0x01;
}
void task1(void *p)
{
while(1) {
if(countingsemaphore!=NULL) {
if(xSemaphoreTake(countingsemaphore,portMAX_DELAY)==pdTRUE) {
sendsserial("Task 1 Takes Semaphore");
sendsserial("\r\n");
sendsserial("\r\n");
}
}
}
}
void task2(void *p)
{
while(1) {
if(countingsemaphore!=NULL) {
if(xSemaphoreTake(countingsemaphore,portMAX_DELAY )==pdTRUE) {
sendsserial("Task 2 Takes Semaphore");
sendsserial("\r\n");
sendsserial("\r\n");
}
}
}
}
void rx1(void)__irq
{
static portBASE_TYPE interrupttask;
unsigned char r;
if(U0IIR&0x04) {
r=U0RBR;
sendsserial("Received Data = ");
U0THR=r;
while(!(U0LSR&0x20));
sendsserial("\r\n");
sendsserial("Going to Give Semaphore From ISR");
sendsserial("\r\n");
xSemaphoreGiveFromISR(countingsemaphore,&interrupttask );
}
VICVectAddr = 0x00;
}
Output
In our next tutorial, we will see how to use the Mutex in the FreeRTOS.
You can also read the below tutorials.
|
|
|

Embedded Software | Firmware | Linux Devic Deriver | RTOS
Hi, I am a tech blogger and an Embedded Engineer. I am always eager to learn and explore tech-related concepts. And also, I wanted to share my knowledge with everyone in a more straightforward way with easy practical examples. I strongly believe that learning by doing is more powerful than just learning by reading. I love to do experiments. If you want to help or support me on my journey, consider sharing my articles, or Buy me a Coffee! Thank you for reading my blog! Happy learning!